While trying to come up with something to program, I looked to prime numbers in my discrete math class and decided to make a simpler prime number calculator. The deeper I delve into the world of prime numbers the more interested I become. The building blocks of all numbers with plentiful applications in cryptography have captured my spare time recently. This is part 1 of my quest for calculating prime numbers. I have no real goal in this quest, other than to expand my knowledge of mathematics and sharpen my skills of programming; it’s the journey that matters, not the destination.
First off some math. What is a prime number?
Prime Number: A positive integer p greater than 1 is called prime if the only positive factors of p are 1 and p. A positive integer that is not prime is called composite.
For example, 42 is not prime, it can be written as the product of the factors 2 and 28. 28 isn’t prime either, it can be written as 2*14. 14 can be written as 2*7. What can 7 be written as? or 2? Nothing, these are primes. Now a useful theorem.
Fundamental Theorem of Arithmetic: every positive integer greater than 1 can be written uniquely as a prime or as a product of two or more primes.
That means 42 can be written as 2*2*2*7, all of which are prime numbers. 105 can be written as 3*5*7, all prime.
Now, how can you tell of a number is prime? Well, if the number is composite, that means it can be divided by some prime number. You can keep a list of prime numbers and then try and divide that number by them all. If it doesn’t divide by any prime numbers, it’s prime itself. For example, we find a list of prime numbers: 2, 3, 5, 7, 11. Now suppose we want to see if the number 13 is prime. We’d do the following,
13 % 2 == 0? If so prime.
13 % 3 == 0? If so prime.
13 % 5 == 0? If so prime.
13 % 7 == 0? If so prime.
13 % 11 == 0? If so prime.
None of these numbers can divide 13, so 13 is prime. When we get into prime numbers like 576,194,557 though, this process will be doing millions of checks on the prime numbers found before, which will be horribly slow.
A quick way to make a huge speed difference is use another handy theorem.
Theorem: If n is a positive composite integer, then n has a prime divisor less than or equal to sqrt(n).
So rather than checking if 576,194,557 is divisible by each prime found before it, we can just check if it’s divisible by any of the primes less than or equal to 24,004.
Before getting down to the programming, one more quick way to make it more efficient is to count by 2’s, since we know all prime numbers are odd. In fact, prime numbers always end in either 1, 3, 7, or 9. Increasing the number you’re checking for primeness by 2 every time can eliminate checking anything that ends with 0, 2, 4, 6, or 8.
Therefore, a simple brute force method for finding primes: create an array (in the heap, because the stack will overflow), and store all the primes you find in it. Increase your candidate number by 2, try to divide it by all the primes in the list, and break out of the loop if you find a number that divides it or if you reach a prime larger than sqrt(candidate). The latter means it’s composite and the former means it’s prime. Keep doing this until you find as many primes as you like. My source code for such a program written in ANSI C can be found here, http://pherricoxide.jumbofx.com/code/simpleprimecalc.c. It’s well commented and should compile with any ANSI C compiler. This is the first of hopefully several prime calculators I’m going to write.
Using this program on a 1.4ghz Intel Core 2 Duo with 2GB RAM, the first 100 million primes are found in about 137 minutes.
The problem is, as the numbers get bigger, this program runs slower and slower. The graph below shows time plotted on the horizontal axis and number of primes found plotted on the vertical. You rapidly find primes in the beginning, but after a while it will inevitably take you long minutes just to find a few primes. Using this method, we hardly have to worry about running out of RAM, because by the time we get 2GB of data (around 200 million primes), the process will be going so slowly it will hardly be worth continuing the search, at least using this brute force method.

Stay tuned for faster prime calculations with better code, better algorithms, and someday perhaps even some cluster computing, as I continue my quest for primes. Until then, here are some prime numbers to spot check your own prime calculating programs with.
1 millionth prime: 15,485,863 (found in 7 seconds)
5 millionth prime: 86,028,121 (found in 112 seconds)
10 millionth prime: 179424673 (found in 5 minutes)
20 millionth prime: 373,587,883 (found in 12 minutes)
30 millionth prime: 573,259,391
40 millionth prime: 776,531,401
50 millionth prime: 982,451,653 (found in 50 minutes)
60 millionth prime: 1,190,494,759
70 millionth prime: 1,400,305,337
80 millionth prime: 1,611,623,773
90 millionth prime: 1,824,261,409
100 millionth prime: 2,038,074,743 (found in 137 minutes)
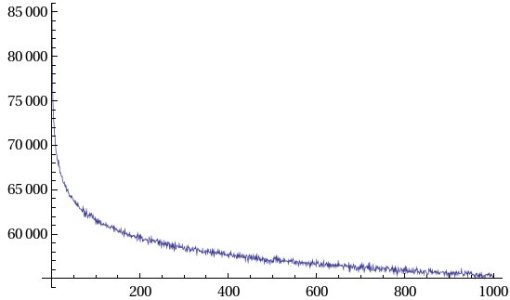 Cousin primes: prime numbers that differ by four. Interestingly, according to some number theory equations called the Hardy–Littlewood conjecture, they are supposed to have about the same distribution as twin primes. My results show it’s quite close, 58,040,262 of them in the first billion primes. The graph is about the same.
Cousin primes: prime numbers that differ by four. Interestingly, according to some number theory equations called the Hardy–Littlewood conjecture, they are supposed to have about the same distribution as twin primes. My results show it’s quite close, 58,040,262 of them in the first billion primes. The graph is about the same.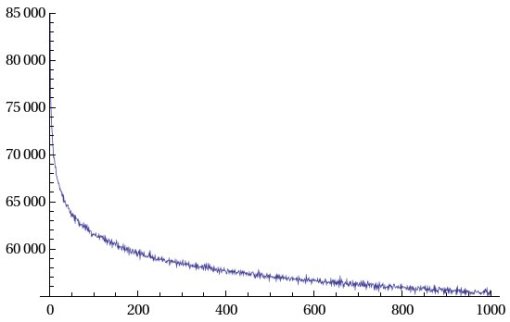 Sexy primes: no, I didn’t come up with the name, the Latin word for 6 is sex, and the math people love to name things in Latin and use Greek symbols. Primes that differ by 6. There are 105,002,853 of them in the first billion, quite a bit more than twin or cousin primes.
Sexy primes: no, I didn’t come up with the name, the Latin word for 6 is sex, and the math people love to name things in Latin and use Greek symbols. Primes that differ by 6. There are 105,002,853 of them in the first billion, quite a bit more than twin or cousin primes.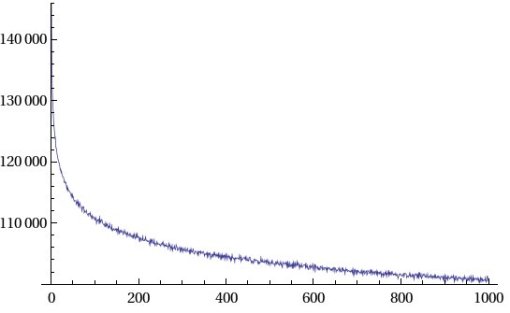 Answer primes: pairs of primes that differ by 42. Okay, I did make this one up. Any scifi fans out there will see the reference. There are 22,729,810 of them in the first billion primes. The graph is at least more interesting than the others due to the fact it’s a larger number. The distance between primes increases as the primes gets bigger.
Answer primes: pairs of primes that differ by 42. Okay, I did make this one up. Any scifi fans out there will see the reference. There are 22,729,810 of them in the first billion primes. The graph is at least more interesting than the others due to the fact it’s a larger number. The distance between primes increases as the primes gets bigger. Some random facts of interest (to weird people like me anyway).
Some random facts of interest (to weird people like me anyway). Of course, primes can’t be odd numbers apart, because that would make them even. That explains the pattern a bit. Still, for something that has baffled mathematicians for centuries, it certainly does seem like there’s a pattern to it. If you draw lines between the points,
Of course, primes can’t be odd numbers apart, because that would make them even. That explains the pattern a bit. Still, for something that has baffled mathematicians for centuries, it certainly does seem like there’s a pattern to it. If you draw lines between the points, Certainly not as pretty.
Certainly not as pretty.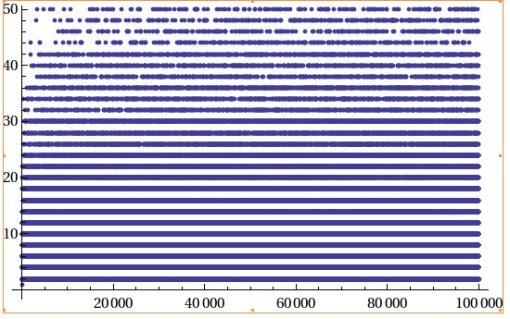 The scale makes this one a bit less interesting. Too much overlap, but Mathematica really doesn’t like big listplots like this. I even crashed it a few times when I tried to do a listplot of 100,000 data plots. 10,000 was pushing it.
The scale makes this one a bit less interesting. Too much overlap, but Mathematica really doesn’t like big listplots like this. I even crashed it a few times when I tried to do a listplot of 100,000 data plots. 10,000 was pushing it.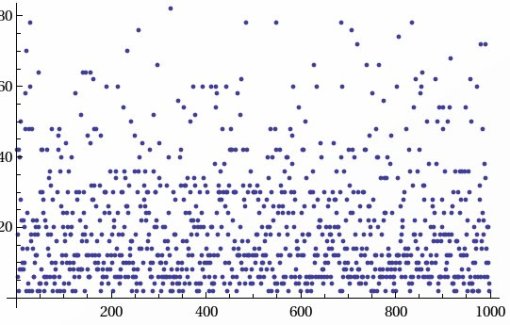 More interesting patterns in primes, the Ulam spiral. Starting at 1 and spiraling outwords from the orgin, you create a graph like so (
More interesting patterns in primes, the Ulam spiral. Starting at 1 and spiraling outwords from the orgin, you create a graph like so ( And then remove all but the primes (
And then remove all but the primes ( And you find an intersting pattern, that the prime numbers tend to lay along some diagnols more oftan than others. Expanding this to 150,000 primes,
And you find an intersting pattern, that the prime numbers tend to lay along some diagnols more oftan than others. Expanding this to 150,000 primes,


 .” First off, I can plug that into Mathematica and get the answer in a few dozen clock cycles, faster than I can even write the first derivative with respect to x. For that matter, faster than I can write the letter ‘x’.
.” First off, I can plug that into Mathematica and get the answer in a few dozen clock cycles, faster than I can even write the first derivative with respect to x. For that matter, faster than I can write the letter ‘x’.